Gaussian Basis Sets - Overview
 From the point of view of ab initio (first principles) electronic structure
methods, a basis set is simply a collection of functions, whose members are
typically associated with one or more of the atoms in a molecule. When people
say that they are "using the 3-21G basis on ethylene" they really mean that
they're performing a calculation with the appropriate carbon and hydrogen 3-21G
basis functions ("3-21G" is the just the name given to this basis set family
by scientists who originally developed it) positioned at the two carbons and
four hydrogens in C2H4, for a total of 26 functions.
From the point of view of ab initio (first principles) electronic structure
methods, a basis set is simply a collection of functions, whose members are
typically associated with one or more of the atoms in a molecule. When people
say that they are "using the 3-21G basis on ethylene" they really mean that
they're performing a calculation with the appropriate carbon and hydrogen 3-21G
basis functions ("3-21G" is the just the name given to this basis set family
by scientists who originally developed it) positioned at the two carbons and
four hydrogens in C2H4, for a total of 26 functions.
Basis sets are a mathematical convenience because the quantum mechanical equations
which describe the behavior of electrons in molecules are most easily solved
by expanding the wavefunction or density in terms of a finite set. Only in specialized
cases, such as diatomic molecules, has it proven computationally feasible to
forego the use of basis sets in favor of fully numerical techniques.
 Along with the sophistication of the approach used in describing the correlated
motions of the electrons in a molecule, basis sets represent one of the two
primary user-selectable input parameters for ab initio programs such
as Gaussian, GAMESS and NWChem. A poorly chosen basis set will typically lead
to large inaccuracies in the computed results or, in some cases, qualitatively
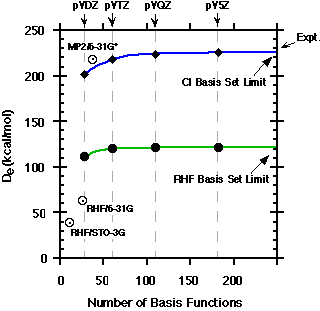
incorrect findings. A simple example is the dissociation energy of N2. The experimental
value of De is 228 kcal/mol, whereas small basis set RHF predicts a value of
39 kcal/mol. Larger basis sets, used with highly correlated methods can come
within 1 - 2 kcal/mol of experiment. Another example is the hydronium cation,
H3O+, which has a pyramidal shape like ammonia. With small basis sets this molecule
is incorrectly predicted to be flat.
Along with the sophistication of the approach used in describing the correlated
motions of the electrons in a molecule, basis sets represent one of the two
primary user-selectable input parameters for ab initio programs such
as Gaussian, GAMESS and NWChem. A poorly chosen basis set will typically lead
to large inaccuracies in the computed results or, in some cases, qualitatively
incorrect findings. A simple example is the dissociation energy of N2. The experimental
value of De is 228 kcal/mol, whereas small basis set RHF predicts a value of
39 kcal/mol. Larger basis sets, used with highly correlated methods can come
within 1 - 2 kcal/mol of experiment. Another example is the hydronium cation,
H3O+, which has a pyramidal shape like ammonia. With small basis sets this molecule
is incorrectly predicted to be flat.
Some basis sets consist of relatively few functions. For example, the STO-3G
basis has only one function per occupied atomic orbital (1s, 2s, 2px, 2py, 2pz).
Others have a large number of functions of different symmetries (e.g. s, p,
d, f...). Basis sets which are too small may lack the flexibility to describe
the basic physics of a problem and can produce qualitatively misleading results,
with no hint of trouble. Likewise, overly large basis sets may waste many hours
of computer time.
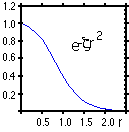
Over the years theoretical chemists have used a variety of different functional
forms as basis functions. Some of the earliest calculations were done with exponential
functions that mimicked the atomic hydrogen orbitals. However, for practical purposes,
nearly all of today's ab initio calculations on polyatomic molecules use
Cartesian Gaussians of the form:
g(r) = N*(x l)*(y m)*(zeta n)*exp(-zeta*r
2),
where N is a normalization constant which insures that the square of the Gaussian
gives a value of 1.0 when integrated over all space, (l,m,n) are integer powers
of the electron's Cartesian coordinates ranging from 0 to some small positive
value, and zeta is an exponent which helps determine the radial size
of the function. The variable r represents the distance of the electron from
the origin of the Gaussian.
Functions with L = l+m+n = 0 are spherically symmetric about the origin and
are known as "s" functions. Similary, the three functions corresponding to l+m+n
= 1 are the p(x), p(y), p(z) functions, etc. The Cartesian Gaussians possess
six functions with l+m+n = 2, from which the five spherical components, d(xy),
d(xz), d(yz), d(xx-yy) and d(2zz-xx-yy), can be constructed. The remaining function
is of spherical symmetry and is customarily deleted. As the total L value increases,
the difference in the number of Cartesian and spherical components increases.
Many electronic structure programs are able to handle either form.
- Exponents - Exponents are the prefactors
multiplying r 2 in the exponential part of the Gaussian. Exponents
are often represented by the Greek character zeta. A small exponent, e.g.
0.01 will produce a diffuse function, whereas a large exponent, e.g. 10,000,
makes for a function which is very tight about the origin (usually an atom).
- Contraction Coefficients - Compared to
the radial solutions of the hydrogen atom that are described in most undergraduate
chemistry texts, individual Gaussians have the wrong behavior at the origin
and die off too rapidly at large distances. However, by combining several
individual Gaussians (sometimes referred to as "primitives" or "Gaussian primitives"
into fixed linear combinations of functions known as "contracted" functions,
it is possible to mimic the shape of the hydrogenic functions, which fall
off as e-(zeta*r) with distance. Because this reduces the number of
variational degrees of freedom, the cost of the calculation, especially post
Hartree-Fock calculations, such as perturbation theory or configuration interaction,
are reduced with only a modest impact on the accuracy.
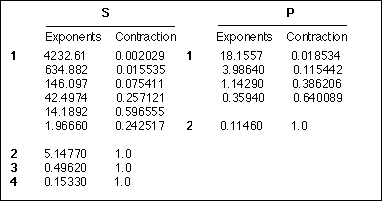
There are two types of contracted basis functions in widespread use today.
In "segemented" contractions a given primitive function appears in no more
than one contracted function. Two examples of segmented contractions are
the STO-3G and the Dunning DZ basis sets, the latter of which is shown here
for the carbon atom.
Segmented contractions became more difficult to construct as you went
further down the periodic table. This led to the development of another
way of contracting Gaussian primitives.
The second category of contracted basis function is referred to as a "general"
contraction. In general contractions a given primitive can appear in more
than one contracted function. Examples of generally contracted basis sets
are the NASA Ames Atomic Natural Orbital (ANO) and the Roos ANO basis sets.
An example from the latter family is shown to the right. Generally contracted
basis sets have a reputation for being more time consuming to use than their
segmented counterparts. This is partially due to the relative scarcity of
integral programs which are designed to handle these basis functions efficiently.
Although it is possible to use general contractions with any integral program,
there will be a penalty to pay with some codes. For example, if there are
10 generally contracted s-symmetry basis functions defined in terms of 20
Gaussian primitives, some codes will interpret this situation as a calculation
over 10 x 20 = 200 primitives.
Finally, some basis sets possess characteristics of both contraction styles.
For the sake of simplicity, these sets are normally referred to as generally
contracted basis sets. The new correlation consistent basis set family developed
by T. H. Dunning, Jr. and co-workers is an example of a hybrid contraction
style.
With this last category of contraction it is sometimes possible to reformat
the basis set so that the performance penalty you're forced to pay for using
generally contracted functions in programs that weren't designed for them
is minimized. In the Ecce Basis Set Tool we refer to this reformatting as
"optimizing" the general contraction.
- Polarization Functions - Gaussians of
a higher symmetry than the ground state occupied atomic orbitals are referred
to as polarization functions. For example, since the first row elements (Li
- Ne) possess occupied s and p atomic orbitals, d, f, g, etc. functions would
be classified as polarization functions. The qualitative importance of polarization
functions is that they permit the molecular wavefunction more flexibility
to distort away from spherical symmetry in the neighborhood of each atom.
The general shapes of the spherical harmonic forms of the basis functions
up through l = 3 (f functions) is shown here.
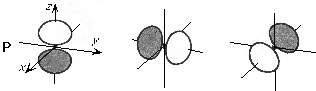
From a practical perspective, the first polarization functions (e.g. a
set of d functions on carbon) are the most important additions one can make
to the basis set beyond the valence s and p functions. At the Hartree-Fock
level of theory, most properties converge to the complete basis set limit
relatively quickly with the addition of more polarization functions. However,
at the correlated level of theory the convergence is typically much slower,
so that many higher l functions are needed in order to reach the complete
basis set limit. In particularly difficult cases, such as the dissociation
energy of N2, basis sets containing d and f polarization functions still
underestimate the true value of De by more than 10 kcal/mol.
As is evident from these pictures, as the l value increases, so does the
number of angular nodes (places where the orbital changes sign).
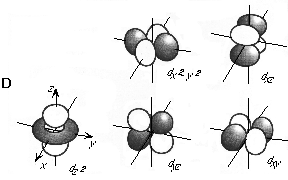
The l = 4 (g) functions have 4 such nodal planes. Although g functions
are not shown, you can imagine that their 3D shapes have gotten to be quite
complex and there are a lot of them. Because of the large number of g functions
and the fact that integrals over g functions are time consuming to compute,
relatively few polyatomic calculations are performed with these functions.
Some programs can perform calculations with two different forms of the
higher l value Gaussians. There are l*(l+1)/2 + (l+1) Cartesian Gaussians,
but only 2*l+1 Spherical Harmonic functions for a given value of l. Thus,
for l greater than 1 (p functions) there are more Cartesian than Spherical
components. The relative numbers of Cartesian and Spherical Gaussians are:
d functions (l=2) 6 Cart. and 5 Spher.,
f functions (l=3) 10 Cart. and 7 Spher.,
g functions (l=4) 15 Cart. and 9 Spher.,
h functions (l=5) 21 Cart. and 11 Spher.

A wide range of special polarization sets have been designed for various
properties or types of calculations.
- Orbital Basis Sets - In the Ecce Basis Set
Tool we distinguish between "Orbital", "Effective Core Potential" (ECP) and
the auxiliary "DFT Fitting" basis sets that are used in some density functional
calculations. As the name implies, "orbital" basis sets are used to expand
the molecular orbitals of a chemical system. This category of basis set has
received a great deal of attention over the past 30 years, resulting in a
very large number of orbital sets in the chemistry literature.
- Effective Core Basis Sets - These basis sets are
designed for use in calculations that replace the inner core electrons, e.g.
1s electrons in carbon, with special projectors that prevent variational collapse
of the remaining electrons. Typically, when ECPs are published there are accompanying
special basis sets that are designed to work with the ECPs. However, in principal
it should be possible to use any orbital basis set (minus the core functions)
with any ECP.
- Fitting Basis Sets - In order to obtain efficiency
in density functional calculations, auxilliary uncontracted basis sets are
used to fit the electron (i.e. charge) density and the exchange-correlation
functional. The area of DFT fitting basis sets is still in its infancy. Thus,
there are relatively few such sets available in the literature.


Ecce Online Help
Revised: November 3, 2002
|
Disclaimer |
 From the point of view of ab initio (first principles) electronic structure
methods, a basis set is simply a collection of functions, whose members are
typically associated with one or more of the atoms in a molecule. When people
say that they are "using the 3-21G basis on ethylene" they really mean that
they're performing a calculation with the appropriate carbon and hydrogen 3-21G
basis functions ("3-21G" is the just the name given to this basis set family
by scientists who originally developed it) positioned at the two carbons and
four hydrogens in C2H4, for a total of 26 functions.
From the point of view of ab initio (first principles) electronic structure
methods, a basis set is simply a collection of functions, whose members are
typically associated with one or more of the atoms in a molecule. When people
say that they are "using the 3-21G basis on ethylene" they really mean that
they're performing a calculation with the appropriate carbon and hydrogen 3-21G
basis functions ("3-21G" is the just the name given to this basis set family
by scientists who originally developed it) positioned at the two carbons and
four hydrogens in C2H4, for a total of 26 functions.

 Along with the sophistication of the approach used in describing the correlated
motions of the electrons in a molecule, basis sets represent one of the two
primary user-selectable input parameters for ab initio programs such
as Gaussian, GAMESS and NWChem. A poorly chosen basis set will typically lead
to large inaccuracies in the computed results or, in some cases, qualitatively
incorrect findings. A simple example is the dissociation energy of N2. The experimental
value of De is 228 kcal/mol, whereas small basis set RHF predicts a value of
39 kcal/mol. Larger basis sets, used with highly correlated methods can come
within 1 - 2 kcal/mol of experiment. Another example is the hydronium cation,
H3O+, which has a pyramidal shape like ammonia. With small basis sets this molecule
is incorrectly predicted to be flat.
Along with the sophistication of the approach used in describing the correlated
motions of the electrons in a molecule, basis sets represent one of the two
primary user-selectable input parameters for ab initio programs such
as Gaussian, GAMESS and NWChem. A poorly chosen basis set will typically lead
to large inaccuracies in the computed results or, in some cases, qualitatively
incorrect findings. A simple example is the dissociation energy of N2. The experimental
value of De is 228 kcal/mol, whereas small basis set RHF predicts a value of
39 kcal/mol. Larger basis sets, used with highly correlated methods can come
within 1 - 2 kcal/mol of experiment. Another example is the hydronium cation,
H3O+, which has a pyramidal shape like ammonia. With small basis sets this molecule
is incorrectly predicted to be flat.